

This puzzle quickly reached fame as the brainteaser now known as the Tower of Hanoi.ĭespite it seeming initially perplexing, in truth the Tower of Hanoi is a problem that even amateur puzzlers can solve with a bit of lateral thinking. However, the catch is, a larger disc can never sit on top of a smaller disc. The aim is to move the tower, one disc at a time, over to the right-hand pole.
HANOI TOWERS FUNCTION SERIES
There are three poles in a row, the one on the left containing a series of discs of decreasing size, with the other two, empty. 1883, a French mathematician named Édouard Lucas came up with an intriguing scenario. Public void solve(int n, String srcTower, String intermediateTower, String destTower) * Recursion to solve Towers of Hanoi problem.
HANOI TOWERS FUNCTION CODE
Please checkout code snippet and algorithm visualization section for more details of the algorithm. As you should be able to verify, to move 'n' disks, minimum number of moves needed are (2^n - 1). Time taken by this algorithm is exponential in nature. To do this, we again make a recursive call - solve(n = n-1, srcTower = intermedTower, intermedTower = srcTower, destTower = destTower).Here again, roles of intermedTower and srcTower are exchanged. Lastly, we want to move 'n-1' disks from intermedTower to destTower using srcTower. At this step, we are basically hitting the base case for recursion.ĥ. After completion of step #3, we make a recursive call solve(n = 1, srcTower = srcTower, intermedTower = intermedTower, destTower = destTower) to move the last disk sitting at srcTower to destTower using intermedTower though intermedTower is not needed in this case. Note how the roles of intermedTower and destTower have changed for solving this puzzle for 'n-1' disks.Ĥ. To do this, we make a recursive call - solve(n = n-1, srcTower = srcTower, intermedTower = destTower, destTower = intermedTower). We want to first move top 'n-1' disks from srcTower to intermedTower using destTower. This is the base case for this recursion.ģ. We move that disk to destTower and return to the calling function. if (n = 1) then the only disk sitting at srcTower can be moved to destTower. Initial call is made to function solve(n = n, srcTower = A, intermedTower = B, destTower = C)Ģ. If function 'solve' takes arguments as number of disks to be moved, source tower(A), intermediate tower(B) and destination tower(C) thenġ. Once we do that following state is reached and we are done.īy careful observation of above steps we can formulate the recursive algorithm to solve this problem. Now from this state, we need to move the two disks sitting at the tower 'B' to tower 'C' using tower 'A'.
HANOI TOWERS FUNCTION FREE
Once we get to this state, the last disk in tower A is free to move to tower 'C' and once we move that disk to tower 'C' we reach the following state. Where top two disks are moved to tower 'B' by making use of tower 'C'(if required). Without caring too much about the details, from the above given state we first want to reach to the following shown state.
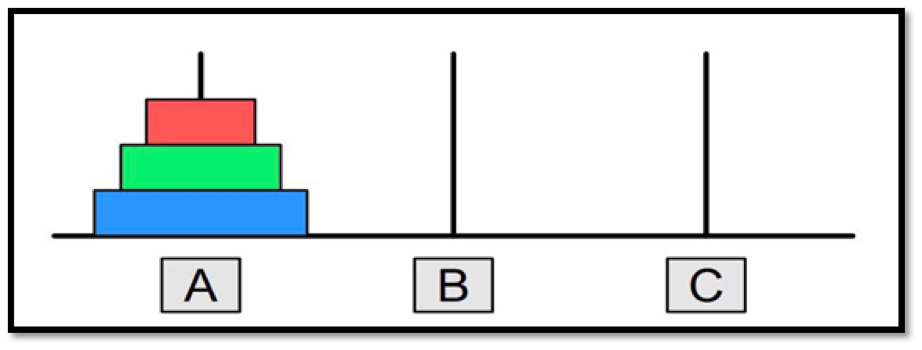
Let's first try to understand the abstract procedure that would help to solve this problem. This is a classic example to understand the intuition of recursion.


 0 kommentar(er)
0 kommentar(er)
